题目描述

给定一个 n × n 的二维矩阵表示一个图像。

将图像顺时针旋转 90 度。

说明：

你必须在原地旋转图像，这意味着你需要直接修改输入的二维矩阵。请不要使用另一个矩阵来旋转图像。

示例 1:

给定 matrix = 
[
  [1,2,3],
  [4,5,6],
  [7,8,9]
],

原地旋转输入矩阵，使其变为:
[
  [7,4,1],
  [8,5,2],
  [9,6,3]
]

示例 2:

给定 matrix =
[
  [ 5, 1, 9,11],
  [ 2, 4, 8,10],
  [13, 3, 6, 7],
  [15,14,12,16]
], 

原地旋转输入矩阵，使其变为:
[
  [15,13, 2, 5],
  [14, 3, 4, 1],
  [12, 6, 8, 9],
  [16, 7,10,11]
]

分析

现在的问题是我们需要对哪些元素进行操作。因为题目要求使用原地算法，这样就不可能对每个元素都操作一遍，因为有的元素被改变过后，后面再使用它的时候它的值已经不是原来的值了，就得不到正确的旋转结果了，因此我们只能对矩阵的部分元素操作。

我们把矩阵看成一圈一圈组成的，然后从外到内，对每一层进行旋转操作就可以了，如下图所示：

根据这张图片，我们可以把整个矩阵分为4个部分，如下图所示：

所以实际上我们只需要操作上边的1/4个矩阵就可以了。

直观地感受一下，可以发现，经过旋转之后：

对每一行来看：

第0行的元素到了最后1列(n-1-0)

第1行的元素到了倒数第2列(n-1-1)

…

第n-1行的元素到了倒数第n列(n-1-(n-1))

对每一列来看：

第0列的元素到了第0行

第1列的元素到了第1行

…

第n-1列的元素到了第n-1行

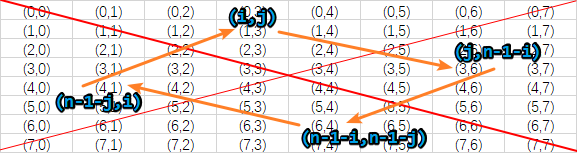
所以我们可以得到一个规律，如果把当前元素的位置用（i, j)来表示，那么经过旋转变换后，这个元素的位置就变到了(j, n-1-i)。

现在转换一下思路，当前元素的位置是(i, j)，那么它是从哪个位置旋转过来的呢？我们可以设一个未知数(x, y)，表示当前元素的上一个位置，(x, y)经过旋转后，位置变为了(i, j)。根据上一步我们总结出来的规律，我们可以得到一个方程：

$$i = y$$

$$j = n-1-x$$

解得

$$x= n-1-j$$

$$y=i$$

所以我们可以得到(i, j)是由(n-1-j, i)变换来的。那么(n-1-j, i)又是由谁变换来的呢？用同样的方法可以得到。以此类推，可以得到一圈四个元素的变换顺序。

源码

class Solution {
    public void rotate(int[][] matrix)
    {
        int n = matrix.length;
        for (int i = 0; i < n / 2; i++) {
            for (int j = i; j < n - 1 - i; j++) {
                int temp = matrix[i][j];
                matrix[i][j] = matrix[n - j - 1][i];
                matrix[n - j - 1][i] = matrix[n - i - 1][n - j - 1];
                matrix[n - i - 1][n - j - 1] = matrix[j][n - i - 1];
                matrix[j][n - i - 1] = temp;
            }
        }

    }
}

测试用例

public static void main(String[] args)
{
    RotateImage ri = new RotateImage();
    int[][] matrix = new int[][]{
            {1,2,3},
            {4,5,6},
            {7,8,9}
    };
    ri.rotate(matrix);
    for (int[] row : matrix) {
        System.out.println(Arrays.toString(row));
    }
}