常用排序算法总结

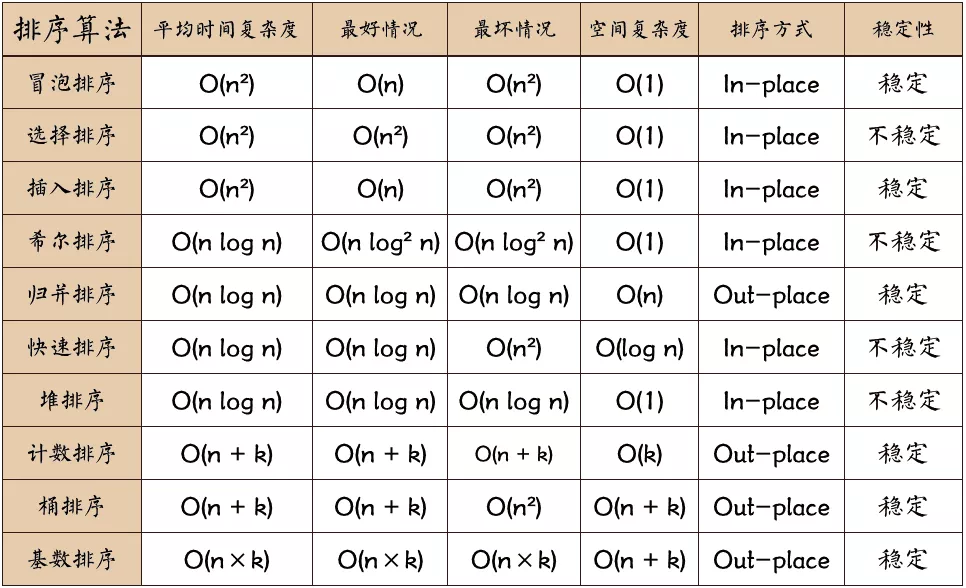
冒泡排序

比较相邻的两个元素，如果前一个元素比后一个元素大，则交换它们的位置。第一趟做完后，最后一个元素肯定是数组中最大的元素。

开始第二趟比较，第二趟比较把最后一个元素排除在外。

重复以上步骤，直到没有一对元素需要比较。

优化点：

冒泡排序的缺点是每一趟比较都需要遍历数组，但是这个缺点可以利用成优点，可以设置一个标志位，记录这一趟遍历数组的过程中是否有交换元素的操作，如果没有交换元素的操作，说明数组已经排序好了，后面的一系列操作都不需要了。

时间复杂度：~N^2^/2

最好情况下：N

public static void bubbleSort (int[] nums) {
    int N = nums.length;
    for (int i = 1; i < N; i++) {
        // 总共需要 N-1 趟遍历使数组排好序
        boolean isSorted = true;
        for (int j = 0; j < N - i; j++) {
            if (nums[j] > nums[j + 1]) {
                swap(nums, j, j + 1);
                isSorted = false;
            }
        }
        if (isSorted) break;
    }
}

选择排序

首先，找到数组中最小的那个元素，其次，将它和数组中第一个元素交换位置（如果第一个元素就是最小的元素，那就和自己交换），再次，在剩余的元素中找到最小的元素，将它与数组中的第二个元素交换位置。如此往复，直到整个数组完成排序。

时间复杂度：

选择排序大约需要 N^2^/2 次比较和 N 次交换

public static void selectSort (int[] nums) {
    int N = nums.length;
    for (int i = 0; i < N; i++) {
        int min = i;
        for (int j = i + 1; j <N; j++) {
            if (nums[j] < nums[min]) {
                min = j;
            }
        }
        swap(nums, i, min);
    }
}

插入排序

遍历数组，将每一个元素放到前面已经排序的元素中合适的位置。在计算机的实现中，为了给插入的元素腾出空间，我们需要将其余所有元素在插入之前都向右移动一位。

时间复杂度：

平均情况下需要 ~N^2^/4 次比较以及~N^2^/4 次交换

最坏情况下需要 ~N^2^/2 次比较以及~N^2^/2 次交换

最好情况下需要 N-1 次比较以及 0 次交换

public static void insertionSort (int[] nums) {
    int N = nums.length;
    for (int i = 1; i < N; i++) {
        for (int j = i; j > 0 && nums[j - 1] > nums[j]; j--) {
            swap(nums, j, j - 1);
        }
    }
}

希尔排序

基于插入排序。

假如打乱数组比较乱，比较大，需要将某一个位置很靠后的元素放到位置比较靠前的地方，但是插入排序只能一个个交换相邻元素，移动速度比较慢。

希尔排序的思想是，使数组中任意间隔为 h 的元素都是有序的，这样的数组被称为 h 有序数组。一个 h 有序数组就是 h 个相互独立的有序数组编织在一起组成的一个数组。

h的选择：我们使用序列h=3*h+1（1，4，13，40，121，364…），使用这个递增序列的希尔排序所需要的比较次数不会超过N的若干倍乘以递增序列的长度。

public static void shellSort (int[] nums) {
    int N  = nums.length;
    int h = 1;
    while (h < N / 3) {
        h = 3 * h + 1;
    }
    while (h >= 1) {
        // 将数组变为 h 有序
        for (int i = h; i < N; i++) {
            // 对 h 有序数组使用 插入排序
            for (int j = i; j >= h && nums[j - h] > nums[j]; j -= h) {
                swap(nums, j, j - h);
            }
        }
        h = h / 3;
    }
}

归并排序

归并排序体现了分治思想。

自顶向下的归并排序

将数组分成两部分，先将左半边数组排序，再将右半边数组排序，将排好序的左右半边数组归并。

时间复杂度：对于长度为N的任意数组，自顶向下的归并排序需要 1/2 NlgN 至 NlgN次比较，最多需要访问数组 6NlgN 次

public class MergeSort extends Sort {
    private static int[] tmp;

    public static void mergeSort (int[] nums) {
        tmp = new int[nums.length];
        mergeSort(nums, 0, nums.length - 1);
    }

    private static void mergeSort (int[] nums, int lo, int hi) {
        if (hi <= lo) return;
        int mid = lo + (hi - lo) / 2;
        mergeSort(nums, lo, mid);
        mergeSort(nums, mid + 1, hi);
        merge(nums, lo, mid, hi);
    }

    private static void merge (int[] nums, int lo, int mid, int hi) {
        int i = lo, j = mid + 1;
        for (int k = lo; k <= hi; k++) {
            tmp[k] = nums[k];
        }
        for (int k = lo; k <= hi; k++) {
            if (i > mid) nums[k] = tmp[j++];
            else if (j > hi) nums[k] = tmp[i++];
            else if (tmp[i] > tmp[j]) nums[k] = tmp[j++];
            else nums[k] = tmp[i++];
        }
    }

    public static void main (String[] args) {
        int[] nums = {3, 44, 38, 5, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48};
        mergeSort(nums);
        assert isSorted(nums);
        System.out.println(Arrays.toString(nums));
    }
}

自底向上的归并排序

先归并最小的数组（只有一个元素的），再成对归并得到的子数组（两个元素），继续归并，直到把整个数组归并到一起。

注意，在归并过程中，可能hi的值会超过数组长度，需要用Math.min(lo + 2 * sz - 1, N - 1)处理一下防止数组越界。

时间复杂度：对于长度为N的任意数组，自底向上的归并排序需要 1/2 NlgN 至 NlgN次比较，最多需要访问数组 6NlgN 次

public class MergeSort extends Sort {
    private static int[] tmp;

    private static void mergeSortBU (int[] nums) {
        int N = nums.length;
        tmp = new int[N];
        for (int sz = 1; sz < N; sz *= 2) {
            for (int lo = 0; lo < N - sz; lo += 2 * sz) {
                merge(nums, lo, lo + sz - 1, Math.min(lo + 2 * sz - 1, N - 1));
            }
        }
    }

    private static void merge (int[] nums, int lo, int mid, int hi) {
        // 将 nums[lo,mid] 和 nums[mid+1,hi] 归并到一起
        int i = lo, j = mid + 1;
        for (int k = lo; k <= hi; k++) {
            tmp[k] = nums[k];
        }
        for (int k = lo; k <= hi; k++) {
            if (i > mid) nums[k] = tmp[j++];
            else if (j > hi) nums[k] = tmp[i++];
            else if (tmp[i] > tmp[j]) nums[k] = tmp[j++];
            else nums[k] = tmp[i++];
        }
    }

    public static void main (String[] args) {
        int[] nums = {3, 44, 38, 5, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48};
        mergeSortBU(nums);
        assert isSorted(nums);
        System.out.println(Arrays.toString(nums));
    }
}

快速排序

• 从数列中挑出一个元素，称为 “基准”（pivot）;
• 重新排序数列，所有元素比基准值小的摆放在基准前面，所有元素比基准值大的摆在基准的后面（相同的数可以到任一边）。在本次切分（partition）退出之后，该基准就处于数列的中间位置；
• 递归地（recursive）把小于基准值元素的子数列和大于基准值元素的子数列排序；

时间复杂度：

将长度为N 的无重复数组排序，快速排序平均需要 ~2NlnN 次比较以及 1/6 的交换

最坏情况：大约N^2^/2次比较

public static void quickSort (int[] nums) {
    shuffle(nums); // 打乱数组，消除对输入的依赖
    quickSort(nums, 0, nums.length - 1);
}

private static void quickSort (int[] nums, int lo, int hi) {
    if (hi <= lo) return;
    int j = partition(nums, lo, hi);
    quickSort(nums, lo, j - 1);
    quickSort(nums, j + 1, hi);
}

private static int partition (int[] nums, int lo, int hi) {
    int pivot = lo;
    int index = pivot + 1;
    for (int i = index; i <= hi; i++) {
        if (nums[i] < nums[pivot]) {
            swap(nums, i, index);
            index++;
        }
    }
    swap(nums, pivot, index - 1);
    return index - 1;
}

堆

用于求解 TopK Elements 问题，也就是 K 个最小元素的问题。可以维护一个大小为 K 的最小堆，最小堆中的元素就是最小元素。最小堆需要使用大顶堆来实现，大顶堆表示堆顶元素是堆中最大元素。这是因为我们要得到 k 个最小的元素，因此当遍历到一个新的元素时，需要知道这个新元素是否比堆中最大的元素更小，更小的话就把堆中最大元素去除，并将新元素添加到堆中。所以我们需要很容易得到最大元素并移除最大元素，大顶堆就能很好满足这个要求。

堆也可以用于求解 Kth Element 问题，得到了大小为 k 的最小堆之后，因为使用了大顶堆来实现，因此堆顶元素就是第 k 大的元素。

快速选择也可以求解 TopK Elements 问题，因为找到 Kth Element 之后，再遍历一次数组，所有小于等于 Kth Element 的元素都是 TopK Elements。

可以看到，快速选择和堆排序都可以求解 Kth Element 和 TopK Elements 问题。

215. 数组中的第K个最大元素

难度：中等

在未排序的数组中找到第 k 个最大的元素。请注意，你需要找的是数组排序后的第 k 个最大的元素，而不是第 k 个不同的元素。

示例 1:

输入: [3,2,1,5,6,4] 和 k = 2
输出: 5

示例 2:

输入: [3,2,3,1,2,4,5,5,6] 和 k = 4
输出: 4

说明:

你可以假设 k 总是有效的，且 1 ≤ k ≤ 数组的长度。

直接调用 Java 排序的方法

排序后直接返回倒数第 K 个数

public int findKthLargest(int[] nums, int k) {
    Arrays.sort(nums);
    return nums[nums.length - k];
}

堆排序法

使用一个大小为 K 的小顶堆，遍历数组，把每个数往小顶堆里面加，小顶堆大小超过K 的时候就把 顶端元素（当前最小值）删掉，数组遍历完成后，留下的小顶堆就是最大的 K 个数，其中堆顶元素就是第 K 大的数。

public int findKthLargest(int[] nums, int k) {
    PriorityQueue<Integer> pq = new PriorityQueue<>(); // 默认是小顶堆
    for (int num : nums) {
        pq.add(num);
        if (pq.size() > k) {
            pq.poll();
        }
    }
    return pq.peek();
}

快速选择法

借用了快速排序中切分的思想，将整个数组切分，如果一个 pivot 的左边正好有 nums.length - k个元素，说明这个元素就是第 K 大的元素。

public int findKthLargest(int[] nums, int k) {
    k = nums.length - k;
    int l = 0, h = nums.length - 1;
    while (l < h) {
        int j = partition(nums, l, h);
        if (j == k) {
            break;
        } else if (j < k) {
            l = j + 1;
        } else {
            h = j - 1;
        }
    }
    return nums[k];
}

private int partition (int[] nums, int lo, int hi) {
    int pivot = lo;
    int index = pivot + 1;
    for (int i = index; i <= hi; i++) {
        if (nums[i] < nums[pivot]) {
            swap(nums, i, index);
            index++;
        }
    }
    swap(nums, pivot, index - 1);
    return index - 1;
}

private void swap (int[] nums, int i, int j) {
    int temp = nums[i];
    nums[i] = nums[j];
    nums[j] = temp;
}

桶排序

347. 前 K 个高频元素

难度：中等

给定一个非空的整数数组，返回其中出现频率前 k 高的元素。

示例 1:

输入: nums = [1,1,1,2,2,3], k = 2
输出: [1,2]

示例 2:

输入: nums = [1], k = 1
输出: [1]

说明：

• 你可以假设给定的 k 总是合理的，且 1 ≤ k ≤ 数组中不相同的元素的个数。
• 你的算法的时间复杂度必须优于 O(n log n) , n 是数组的大小。

• 先把每个元素出现的频率放到一个HashMap里面记录，键为元素值，值为出现的频率
• 设置一系列桶，每个桶里面存放出现相同频率的元素
• 从后往前（从大到小）遍历这一系列桶，找到出现频率最高的K个元素

public List<Integer> topKFrequent(int[] nums, int k) {
    Map<Integer, Integer> frequencyMap = new HashMap<>();
    for (int num : nums){
        frequencyMap.put(num, frequencyMap.getOrDefault(num,0) + 1);
    }

    List<Integer>[] bucket = new ArrayList[nums.length + 1];
    for (Integer key : frequencyMap.keySet()){
        int freq = frequencyMap.get(key);
        if(bucket[freq] == null)
            bucket[freq] = new ArrayList<>();
        bucket[freq].add(key);
    }

    List<Integer> TopK = new ArrayList<>();
    for (int i = bucket.length - 1; i > 0 && TopK.size() < k; i--){
        if(bucket[i] == null)
            continue;
        if(bucket[i].size() < (k - TopK.size())){
            TopK.addAll(bucket[i]);
        }else{
            TopK.addAll(bucket[i].subList(0,k-TopK.size()));
        }
    }
    return TopK;
}

451. 根据字符出现频率排序

难度：中等

给定一个字符串，请将字符串里的字符按照出现的频率降序排列。

示例 1:

输入:
"tree"

输出:
"eert"

解释:
'e'出现两次，'r'和't'都只出现一次。
因此'e'必须出现在'r'和't'之前。此外，"eetr"也是一个有效的答案。

示例 2:

输入:
"cccaaa"

输出:
"cccaaa"

解释:
'c'和'a'都出现三次。此外，"aaaccc"也是有效的答案。
注意"cacaca"是不正确的，因为相同的字母必须放在一起。

示例 3:

输入:
"Aabb"

输出:
"bbAa"

解释:
此外，"bbaA"也是一个有效的答案，但"Aabb"是不正确的。
注意'A'和'a'被认为是两种不同的字符。

• 先把每个元素出现的频率放到一个HashMap里面记录，键为字母，值为出现的频率
• 设置一系列桶，每个桶里面存放出现相同频率的元素
• 从后往前（从大到小）遍历这一系列桶，组成一个新的字符串

public String frequencySort (String s) {
    HashMap<Character,Integer> frequencyMap = new HashMap<>();
    for (char c : s.toCharArray()) {
        frequencyMap.put(c, frequencyMap.getOrDefault(c, 0) + 1);
    }

    List<Character>[] bucket = new ArrayList[s.length() + 1];
    for (Character character : frequencyMap.keySet()) {
        int frequency = frequencyMap.get(character);
        if (bucket[frequency] == null) {
            bucket[frequency] = new ArrayList();
        }
        bucket[frequency].add(character);
    }
    StringBuilder ans = new StringBuilder();
    for (int i = bucket.length - 1; i > 0; i--) {
        if (bucket[i] == null)
            continue;
        for (Character character : bucket[i]) {
            for (int j = 0; j < i; j++) {
                ans.append(character);
            }

        }
    }
    return ans.toString();

}

荷兰国旗问题

三向切分问题

75. 颜色分类

难度：中等

给定一个包含红色、白色和蓝色，一共 n 个元素的数组，原地对它们进行排序，使得相同颜色的元素相邻，并按照红色、白色、蓝色顺序排列。

此题中，我们使用整数 0、 1 和 2 分别表示红色、白色和蓝色。

注意:
不能使用代码库中的排序函数来解决这道题。

示例:

输入: [2,0,2,1,1,0]
输出: [0,0,1,1,2,2]

进阶：

• 一个直观的解决方案是使用计数排序的两趟扫描算法。

   首先，迭代计算出0、1 和 2 元素的个数，然后按照0、1、2的排序，重写当前数组。
  

• 你能想出一个仅使用常数空间的一趟扫描算法吗？

把 0 都放到最前面，2都放到最后面

public void sortColors (int[] nums) {
    int zero = -1, one = 0, two = nums.length;
    while (one < two) {
        if (nums[one] == 0) {
            exch(nums, ++zero, one++);
        } else if (nums[one] == 2) {
            exch(nums, one, --two);
        } else {
            ++one;
        }
    }
}
private static void exch (int[] nums, int i, int j) {
    int temp = nums[i];
    nums[i] = nums[j];
    nums[j] = temp;
}