算法与数据结构数学

LeetCode

发布日期: 2019-09-16

文章字数: 2.7k

阅读时长: 11 分

阅读次数:

素数分解

每一个数都可以分解成素数的乘积，例如 84 = 22 31 50 71 110 130 170 * …

整除

令 x = 2m0 3m1 5m2 7m3 11m4 * …

令 y = 2n0 3n1 5n2 7n3 11n4 * …

如果 x 整除 y（y mod x == 0），则对于所有 i，mi <= ni。

最大公约数或最小公倍数

最大公约数

greatest common divisor，gcd

辗转相除法

int gcd(int a, int b) {
    return b == 0 ? a : gcd(b, a % b);
}

最小公倍数

least common multiple， lcm

int lcm(int a, int b) {
    return a * b / gcd(a, b);
}

204. 计数质数

统计所有小于非负整数 n 的质数的数量。

示例:

输入: 10
输出: 4
解释: 小于 10 的质数一共有 4 个, 它们是 2, 3, 5, 7 。

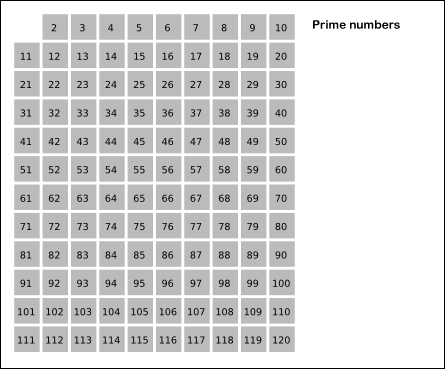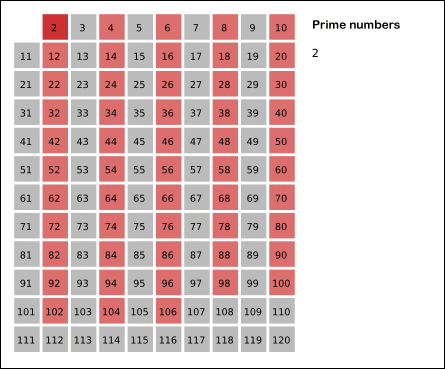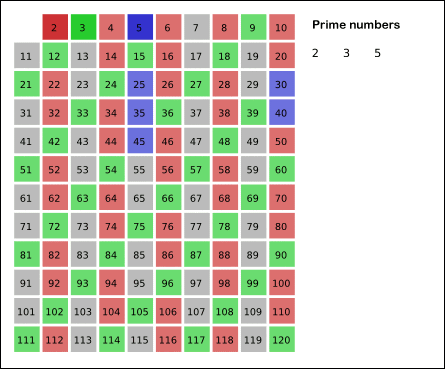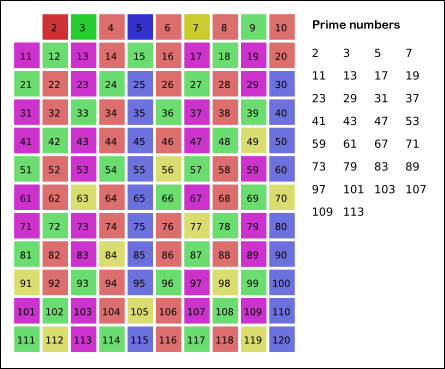
埃拉托斯特尼筛法:

public int countPrimes(int n) {
    boolean[] notPrimes = new boolean[n + 1];
    int count = 0;
    for (int i = 2; i < n; i++) {
        if (notPrimes[i]) {
            continue;
        }
        count++;
        // 从 i * i 开始，因为如果 k < i，那么 k * i 在之前就已经被去除过了
        for (long j = (long) (i) * i; j < n; j += i) {
            notPrimes[(int) j] = true;
        }
    }
    return count;
}

进制转换

504. 七进制数

难度：简单

给定一个整数，将其转化为7进制，并以字符串形式输出。

示例 1:

输入: 100
输出: "202"

示例 2:

输入: -7
输出: "-10"

使用常规的取余，得到最后一位。

public String convertToBase7 (int num) {
    if (num == 0) {
        return "0";
    }
    boolean isNegative = num < 0;
    if (isNegative) {
        num = -num;
    }
    StringBuilder sb = new StringBuilder();
    while (num != 0) {
        sb.append(num % 7);
        num /= 7;
    }
    String ans = sb.reverse().toString();
    return isNegative ? "-" + ans : ans;
}

405. 数字转换为十六进制数

难度：简单

给定一个整数，编写一个算法将这个数转换为十六进制数。对于负整数，我们通常使用补码运算方法。
注意:

十六进制中所有字母( af )都必须是小写。
十六进制字符串中不能包含多余的前导零。如果要转化的数为0，那么以单个字符 ‘0’ 来表示；对于其他情况，十
六进制字符串中的第一个字符将不会是0字符。
给定的数确保在32位有符号整数范围内。
不能使用任何由库提供的将数字直接转换或格式化为十六进制的方

示例 1：

输入:
26

输出:
"1a"

示例 2：

输入:
-1

输出:
"ffffffff"

与二进制数0b1111相与，得到最后一位，0b开头的数用来表示二进制数。

public String toHex (int num) {
    char[] map = {'0', '1', '2', '3', '4', '5', '6', '7', '8', '9', 'a', 'b', 'c', 'd', 'e', 'f'};
    if (num == 0) {
        return "0";
    }
    StringBuilder sb = new StringBuilder();
    while (num != 0) {
        sb.append(map[num & 0b1111]);
        num >>>= 4;
    }
    return sb.reverse().toString();
}

168. Excel表列名称

难度：简单

给定一个正整数，返回它在 Excel 表中相对应的列名称。

例如，

    1 -> A
    2 -> B
    3 -> C
    ...
    26 -> Z
    27 -> AA
    28 -> AB 
    ...

示例 1:

输入: 1
输出: "A"

示例 2:

输入: 28
输出: "AB"

示例 3:

输入: 701
输出: "ZY"

实际上就是一个26进制的问题。因为是从1开始的，所以要将初始的 n 减一处理。

public String convertToTitle (int n) {
    if (n == 0) {
        return "";
    }
    n--;
    return convertToTitle(n / 26) + (char) (n % 26 + 'A');
}

阶乘

172. 阶乘后的零

难度：简单

给定一个整数 n，返回 n! 结果尾数中零的数量。

示例 1:

输入: 3
输出: 0
解释: 3! = 6, 尾数中没有零。

示例 2:

输入: 5
输出: 1
解释: 5! = 120, 尾数中有 1 个零.

说明: 你算法的时间复杂度应为 O(log n) 。

尾部的0肯定是2*5造成的，并且阶乘中，2的数量肯定比5多，所以只需要统计5的个数即可。

对于一个数 N，它所包含 5 的个数为：N/5 + N/5^2^ + N/5^3^ + …，其中 N/5 表示不大于 N 的数中 5 的倍数贡献一个 5，N/5^2^ 表示不大于 N 的数中 5^2^ 的倍数再贡献一个 5 …。

比如说26，小于 26 的数中：

5的倍数有 5，10，15，20，25，所以 N/5 = 5，贡献了 5个5 ；

5^2^的倍数有25，所以N/5^2^=1，再贡献1个5；

总共就是6个5。

递归法：

public int trailingZeroes (int n) {
    return n == 0 ? 0 : n / 5 + trailingZeroes(n / 5);
}

迭代法：

public int trailingZeroes (int n) {
    int ans = 0;
    while(n >= 5){
        ans += n/5;
        n /= 5;
    }
    return ans;
}

字符串加法减法

67. 二进制求和

难度：简单

给定两个二进制字符串，返回他们的和（用二进制表示）。

输入为非空字符串且只包含数字 1 和 0。

示例 1:

输入: a = "11", b = "1"
输出: "100"

示例 2:

输入: a = "1010", b = "1011"
输出: "10101"

分别取两个指针，从字符串的末尾往头部遍历，使用常规的除法和取余，将结果加入到StringBuffer。

public String addBinary(String a , String b)
{
    StringBuffer sb = new StringBuffer();
    int i = a.length() - 1, j = b.length() - 1;
    int carry = 0;
    while (i >= 0 || j >= 0)
    {
        int sum = carry;
        if (i >= 0)
            sum += a.charAt(i--) - '0';
        if (j >= 0)
            sum += b.charAt(j--) - '0';
        sb.append(sum % 2);
        carry = sum / 2;

    }
    if (carry != 0)
        sb.append(carry);
    return sb.reverse().toString();

}

415. 字符串相加

难度：简单

给定两个字符串形式的非负整数 num1 和num2 ，计算它们的和。

注意：

num1 和num2 的长度都小于 5100.
num1 和num2 都只包含数字 0-9.
num1 和num2 都不包含任何前导零。
你不能使用任何內建 BigInteger 库，也不能直接将输入的字符串转换为整数形式。

与上一题类似，但是这一题是十进制。

分别取两个指针，从字符串的末尾往头部遍历，使用常规的除法和取余，将结果加入到StringBuffer。

public String addStrings (String num1, String num2) {
    StringBuilder sb = new StringBuilder();
    int carry = 0;
    int i = num1.length() - 1, j = num2.length() - 1;
    while (i >= 0 || j >= 0 || carry == 1) {
        int x = i < 0 ? 0 : num1.charAt(i--) - '0';
        int y = j < 0 ? 0 : num2.charAt(j--) - '0';
        sb.append((x + y + carry) % 10);
        carry = (x + y + carry) / 10;
    }
    return sb.reverse().toString();
}

相遇问题

462. 最少移动次数使数组元素相等 II

难度：中等

给定一个非空整数数组，找到使所有数组元素相等所需的最小移动数，其中每次移动可将选定的一个元素加1或减1。您可以假设数组的长度最多为10000。

例如:

输入:
[1,2,3]

输出:
2

说明：
只有两个动作是必要的（记得每一步仅可使其中一个元素加1或减1）： 

[1,2,3]  =>  [2,2,3]  =>  [2,2,2]

将每个数移动到中位数是步数最少的。

设 m 为中位数。a 和 b 是 m 两边的两个元素，且 b > a。要使 a 和 b 相等，它们总共移动的次数为 b - a，这个值等于 (b - m) + (m - a)，也就是把这两个数移动到中位数的移动次数。

public int minMoves2 (int[] nums) {
    Arrays.sort(nums);
    int ans = 0;
    int l = 0, r = nums.length - 1;
    while (l < r) {
        ans += nums[r] - nums[l];
        l++;
        r--;
    }
    return ans;
}

多数投票问题

169. 求众数

难度：简单

给定一个大小为 n 的数组，找到其中的众数。众数是指在数组中出现次数大于 ⌊ n/2 ⌋ 的元素。

你可以假设数组是非空的，并且给定的数组总是存在众数。

示例 1:

输入: [3,2,3]
输出: 3

示例 2:

输入: [2,2,1,1,1,2,2]
输出: 2

方法一：

排序数组，正中间那个数就是众数。

public int majorityElement(int[] nums) {
    Arrays.sort(nums);
    return nums[nums.length / 2];
}

方法二：Boyer-Moore 投票算法

设置一个计数器，和一个候选者。

遍历数组，如果当前元素跟候选者相同，计数器加一，否则减一。

当计数器为0时，候选者变成下一元素。

遍历完成后，候选者就是我们找的众数。

public int majorityElement(int[] nums) {
    int majority = nums[0];
    int count = 0;
    for (int num : nums) {
        if (count == 0) {
            majority = num;
        }
        count += (num == majority ? 1 : -1);
    }
    return majority;
}

其他

367. 有效的完全平方数

难度：简单

给定一个正整数 num，编写一个函数，如果 num 是一个完全平方数，则返回 True，否则返回 False。

说明：不要使用任何内置的库函数，如 sqrt。

示例 1：

输入：16
输出：True

示例 2：

输入：14
输出：False

生成序列的方法：

完全平方数序列：1，4，9，16，25…

它们的间隔：1，3，5，7，9…

public boolean isPerfectSquare (int num) {
    int delta = 1;
    while (num > 0) {
        num -= delta;
        delta += 2;
    }
    return num == 0;
}

二分查找法：

如果一个数N是完全平方数，那么在小于 N 的数中，肯定存在 sqrt(N)，用二分查找找这个数，如果找到了，N就是完全平方数，找不到就不是。

public boolean isPerfectSquare (int num) {
    long left = 1, right = num;
    if (num == 1) {
        return true;
    }
    while (left <= right) {
        long mid = left + (right - left) / 2;
        if (mid * mid == num) {
            return true;
        } else if (mid * mid > num) {
            right = mid - 1;
        } else {
            left = mid + 1;
        }
    }
    return false;
}

238. 除自身以外数组的乘积

难度：中等

给定长度为 n 的整数数组 nums，其中 n > 1，返回输出数组 output ，其中 output[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积。

示例:

输入: [1,2,3,4]
输出: [24,12,8,6]

说明: 请不要使用除法，且在 O(n) 时间复杂度内完成此题。

进阶：
你可以在常数空间复杂度内完成这个题目吗？（出于对空间复杂度分析的目的，输出数组不被视为额外空间。）

一个数对应的output = 这个数左边的数的乘积 * 这个数右边的数的乘积

public int[] productExceptSelf (int[] nums) {
    int n = nums.length;
    int left = 1;
    int[] ans = new int[n];
    Arrays.fill(ans, 1);
    for (int i = 1; i < n; i++) {
        left *= nums[i - 1];
        ans[i] *= left;
    }
    int right = 1;
    for (int i = n - 2; i >= 0; i--) {
        right *= nums[i + 1];
        ans[i] *= right;
    }
    return ans;
}

628. 三个数的最大乘积

难度：简单

给定一个整型数组，在数组中找出由三个数组成的最大乘积，并输出这个乘积。

示例 1:

输入: [1,2,3]
输出: 6

示例 2:

输入: [1,2,3,4]
输出: 24

注意:

给定的整型数组长度范围是[3,104]，数组中所有的元素范围是[-1000, 1000]。
输入的数组中任意三个数的乘积不会超出32位有符号整数的范围。

给定的数组中可能负数。

假如对数组排序，最大三个数的乘积，要么是最大的三个数相乘，要么是最小的两个数（两个负数）乘最大的一个数（正数）。

public int maximumProduct (int[] nums) {
    int max1 = Integer.MIN_VALUE;
    int max2 = Integer.MIN_VALUE;
    int max3 = Integer.MIN_VALUE;
    int min1 = Integer.MAX_VALUE;
    int min2 = Integer.MAX_VALUE;
    for (int num : nums) {
        if (num > max1) {
            max3 = max2;
            max2 = max1;
            max1 = num;
        } else if (num > max2) {
            max3 = max2;
            max2 = num;
        } else if (num > max3) {
            max3 = num;
        }

        if (num < min1) {
            min2 = min1;
            min1 = num;
        } else if (num < min2) {
            min2 = num;
        }
    }
    return Math.max(max1 * max2 * max3, min1 * min2 * max1);
}